[Un peu de maths?] L’énigme des chapeaux – 2

Whaou, ça fait un sacré bail que je n’ai pas parlé de maths par ici ! En partie parce que j’avais plein d’autres choses à dire, et en partie parce que je ne savais pas sous quel angle attaquer ce deuxième volet : tu t’en souviens peut-être, il y a maintenant quelques mois j’ai organisé un petit concours, et je te demandais de me donner une solution à l’énigme des chapeaux. J’ai ensuite fait un article qui expliquait la version mathématique pour le cas de deux couleurs (des chapeaux noirs et des chapeaux blancs), et j’avais envie de te présenter la version plus globale, avec plus de couleurs.

Je vais éviter de tout réexpliquer ici, pour te rafraîchir la mémoire le premier article est par là !

Pour faire plus simple, on va s’intéresser au cas de trois couleurs de chapeaux, disons noir, blanc et rouge. Je te rappelle donc qu’on a dix personnes en rond, avec des chapeaux soit noirs, soit blancs, soit rouges, et qu’on voit les chapeaux de tout le monde sauf le sien. A tour de rôle, chacun doit dire à haute voix une couleur, et si ce n’est pas celle de son chapeau on le tue. Et je prétends que là encore, comme dans le cas à deux couleurs, il est possible d’élaborer une stratégie qui sauve à tout les coups tout le monde sauf le premier à prendre la parole !

Kézako le modulo ?

Avant d’entrer dans les détails, il faut qu’on discute d’une notion mathématique bien sympa mais plutôt obscure au premier abord : le modulo. Petite remise en contexte : la première fois que j’ai appris l’existence du modulo, j’étais en première année de maths à l’université, dans les premières semaines de cours, et voilà la définition qu’on nous a donnée : 

C’est obscur pour toi ? Eh bien pour moi aussi à l’époque, je t’assure. Je ne connaissais pas la moitié de ces symboles, je n’avais aucune idée de la structure de cette phrase, et je n’avais aucun exemple pour illustrer le propos, bref un bon truc bien opaque. Tu te demandes des fois ce que ça fait d’étudier les maths ? Ben c’est exactement ça, à peu près tout le temps.

J’ai donc été rendre visite à mon grand ami internet, qui a fini par éclairer ma lanterne. Si on prend une montre et qu’on regarde tourner les aiguilles depuis minuit : on va commencer par 1h, puis 2h, etc.. jusqu’à midi, et ensuite 13h va être équivalent à 1, 14h va être équivalent à 2, … et minuit équivalent à midi, parce qu’on a 24h dans une journée mais que notre cadran n’en représente que douze. Dans ce cas précis, on est en train de compter modulo 12 (on dit alors qu’on est en base 12).

Pour faire un exemple plus simple à écrire, prenons du modulo 3. Par convention, plutôt que de dire qu’on a les boîtes 1, 2 et 3, on préfère commencer à 0 (on a donc les boîtes [0], [1] et [2]). Comme pour les heures, on range donc nos chiffres dans ces trois boîtes, en repassant à [0] chaque fois qu’on a mis un chiffre dans la boîte [2], comme ça :

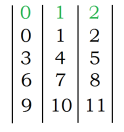
Chaque boîte est appelée une classe (d’équivalence). En modulo 3, on a donc trois classes d’équivalence, et tous les chiffres de la même classe sont dit équivalents (ici, par exemple, 3 est équivalent à 6 et à 9, dans la classe [0]).

Si tu veux imaginer les choses autrement, tu peux aussi le faire en ligne :

Tu t’en doutes peut-être, il y a une explication mathématique derrière cette notion de modulo (et c’est ce qui va nous permettre de comprendre la toute première définition que mon généreux prof de maths m’avait balancée sans explication). En fait, la classe, c’est le reste de la division du chiffre par la base. Si on est en base 3, si on divise 5 par 3 on a un reste de 2, et on peut constater qu’effectivement, 5 est rangé dans la classe [2]. Et si on divise 6 par 3, on a un reste de 0, ce qui veut bien dire que 6 va dans la classe [0]. Tu suis ?

Si on revient à la définition formelle, ce qu’il faut comprendre c’est « r est équivalent à s modulo m si et seulement si m divise (r-s) ». Je n’entre pas dans les détails parce que ce n’est pas très important ici, mais ça revient à dire que s est le reste de la division de r par m. (Eh oui, les maths c’est une langue, il faut comprendre la structure et le vocabulaire…)

Retour à nos chapeaux

Bien, maintenant que la théorie est posée, on peut établir notre système avec nos pauvres gaillards qui n’ont pas très envie de mourir avec leur chapeau coloré sur la tête. On va reprendre mon super schéma du premier article, en rajoutant du rouge.

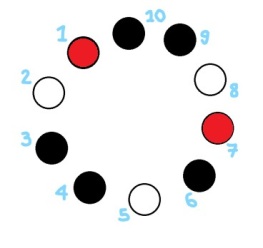
Avant toute chose, nos dix compagnons vont établir un code. Disons :

rouge = [0], noir = [1], blanc = [2].

Que va faire numéro 1, qui voit tous les chapeaux à part le sien ? Eh bien dans un premier temps, il va additionner les chapeaux des autres avec le code prédéfini : ici on a donc (dans l’ordre) 2 + 1 + 1 + 2 + 1 + 0 + 2 + 1 + 1 = 11. Ensuite, il va transformer cette somme modulo 3, et un petit coup d’oeil au tableau de tout à l’heure te permettra de dire que 11 modulo 3 vaut [2] (ou plutôt : 11 = 2 mod 3 si on veut parler en maths). Or [2], c’est le code pour « blanc ». Numéro 1 va donc dire à haute voix « Blanc« . (Malheureusement, ce n’est pas la couleur de son chapeau, mais on savait déjà que le premier risquait de se sacrifier).

Numéro 2, fort de cette information, va faire un rapide calcul mental dans sa grande intelligence : il sait que numéro 1 ne voyait pas son propre chapeau, alors il additionne tout ce qu’il voit SAUF le chapeau de numéro 1, ce qui donne 1 + 1 + 2 + 1 + 0 + 2 + 1 + 1 = 9. On sait désormais que 9 modulo 3, ça fait [0]. Alors il faut compléter ce total pour arriver à ce que voyait numéro 1  :comme il avait compté [2], c’est qu’il voyait en plus le chapeau de numéro 2, qui est forcément de valeur [2]. Numéro 2 dit donc « Blanc » et sauve ses miches.

Numéro 3 va aussi compter tous les chapeaux sauf celui de numéro 1, pour arriver à un total de 10 = [1]. Puisque numéro 1 avait vu [2], c’est qu’il voyait encore un chapeau de valeur [1] : numéro 3 va donc dire « Noir », et ainsi de suite.

C’est un peu difficile de l’expliquer par écrit, j’espère que tu as compris quelque chose à tout ce charabia. Et en fait, tu peux te rendre compte que dans le cas tout simple à seulement deux couleurs, on faisait la même chose : compter en modulo 2, c’est comme compter en binaire et donc classer d’un côté les chiffres pairs et de l’autre les impairs. De la même manière, on peut résoudre ce problème pour n’importe quel nombre fini de couleurs de chapeaux (si on est très, très bon en calcul mental), en sauvant à chaque fois tout le monde sauf le premier.

Et les mathématiciens ont même poussé le délire jusqu’à imaginer un nombre infini de couleurs, mais là vraiment je vais t’épargner (ne me remercie pas). Oh et puis tu sais quoi ? J’ai même trouvé un remix électro de « Chapi Chapo » pour clore cette explication (là tu peux me remercier, par contre)(je décline toute responsabilité en cas de saignement des oreilles).